On a series of centers of any given triangle

Given any triangle T and any positive integer n >=3, we can define a center C_n of T that is the center of gravity of the largest regular n-gon that is contained in T. For large n, C_n tends to the incenter of T.

Question:If we connect these C_n's with a smooth curve, what will be the curve on which all C_n's lie? Is it a spiral converging to the incenter?

Note: One can think of a similar series of centers of smallest regular n_gons that contain T - and this set might give a more interesting smooth curve when joined.

Question on inscribed triangles - and on outer triangles.

Given a planar convex body C, we can define 2 inscribed triangles:
T_a - inscribed triangle of maximum area
T_r - inscribed triangle with largest incircle
Question 1: Are these 2 triangles different from each other for a general C? In cases where the optimal triangles are different, one can try to quantify the difference.
Question 2: Corresponding to these 2 contained triangles, we can think of 2 containing triangles that minimize area and inradius and ask whether those 2 external triangles are distinct in general.
Note 2: The inscribed (containing) triangle with largest (smallest) area is also the inscribed triangle with the largest area Steiner in-ellipse (smallest area Steiner-circumellipse).
Answer to Question 1:

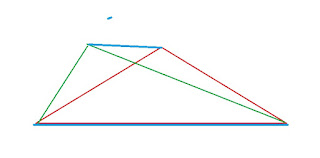
Consider the quadrilateral above. The top left vertex is very slightly higher than the top right vertex - and these two vertices have a substantial x separation. So, the green triangle is the largest area triangle inscribed in the quad (by a small margin) and the red triangle which is isosceles has the largest incircle (note that the inradius of a triangle = area / semiperimeter). This means answer to question 1 above is "the two triangles need not be identical".

Guess on question 2:

Consider a hexagon formed by the itnersection of the two triangles in answer 1 (one of them an isosceles). Then for this hexagon, the smallest area containing triangle would be isosceles one and the other triangle would be another container with slightly larger area but with smaller incircle.

Note: The Steiner circumellipse of a triangle is the containing ellipse with least area but it is not usually the containing ellipse with least perimeter. This follows from the center of the Steiner ellipse being the centroid of the triangle - for a thin and long isosceles triangle, the containing ellipse with least perimeter will have its center close to the mid point of the altitude of the triangle thru the apex and not the centroid. That brings up the question of how to find the that container for a triangle.

Monsky's Theorem - variants

An earlier attempt to ask questions beyond this theorem is here .

Monsky's theorem: it is not possible to dissect a square into an odd number of equal area triangles (Note: this implies no rectangle supports such a dissection).

Question: What about cutting a square into triangles of equal perimeter? For what n can a square be cut into n equal perimeter triangles?

Remark: This discussion shows the dissection of a rectangle into 7 triangles of equal perimeter; so there *might* not be a pattern like Monsky theorem for dissection of a square into triangles of equal perimeter.

Observations: It is easy to see that any triangle can be cut into n triangles of equal area for ANY n and as Monsky proved, a square allows such a partition into equal area triangles only for even n. Moreover, by patching together 3 triangles of equal area that share a vertex and with adjacent triangles sharing an edge, one can form a convex pentagon that can be cut into any n number of triangles all of equal area where n is a multiple of 3.

Question: Can one assert that any convex polygon allows partition into *some* finite number n of equal area triangles? Note: If this claim is true, any convex polygon will allow partition into n equal area triangles for infinitely many different values of n.
Are there convex polygons which support more equal area triangulations than the square and less than the triangle? Are there convex polygons which allow partition into say, only odd numbers of equal area triangles?

Further question: What if we need the triangular pieces all to have equal area and equal perimeter? For example, does this claim hold: Any convex polygon will allow partition into some finite number n of triangles all of same area and perimeter (this is a stronger version of a claim given a little above)?